Synopsis

This project is concerned with the creation of new one-way trapdoor functions and cryptographic primitives based on finite simple semirings.

The study of one-way trapdoor functions is interesting both from a theoretical and from a practical point of view. Our research involves techniques from different parts of algebra and discrete mathematics, such as the theory of finite rings and semirings, the theory of semigroups, and lattice theory. Applications of this research could lead to new cryptographic protocols of potential interest to industry and government.

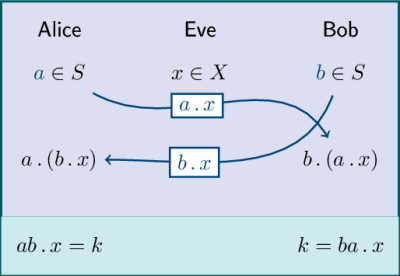It has been observed that the Diffie-Hellman key agreement protocol can be generalized to the context of semigroup actions, and people recently started to investigate alternatives to the discrete logarithm problem.

In this project we plan to investigate semigroup actions which have finite simple semirings as building blocks. Semirings appear to be well-suited for cryptographic purposes, because they have enough structure for a sensible matrix multiplication, but they are resistant to common analytical tools for fields and rings. Simple semirings furthermore avoid a Pohlig-Hellman analogous reduction attack.

The recent concrete classification of finite simple semirings by Zumbrägel provide new tools to progress in this direction. Its proof was inspired and uses many methods of finite ring theory. However, it appears that the diversity of semirings is still far from understood, and we believe that deep insights from ring theory can lead to secure and efficient cryptosystems based on semirings.